上节我们已经学习了如何从数据集中创建树,然而字典的表示形式非常不易于理解,而且直接绘制图形也比较困难。本节我们将使用Matplotlib库创建树形图。决策树的主要优点就是直观易于理解,如果不能将其直观地显示出来,就无法发挥其优势。
决策树的范例:
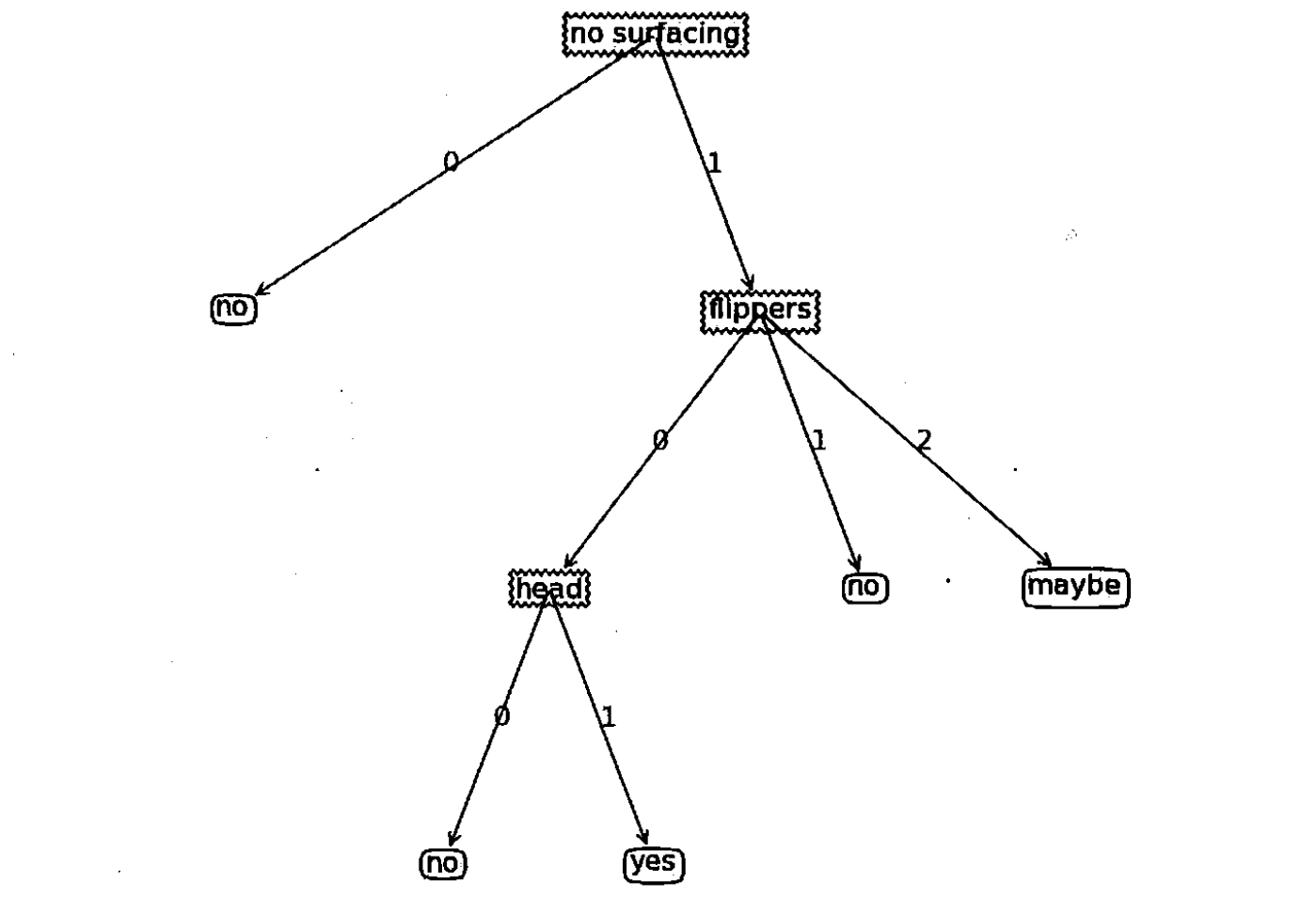
2. 在Python中使用Matplotlib注解绘制树形图
2.1 Matplotlib注解
Matplotlib提供了一个注解工具annotations,它可以在数据图形上添加文本注释。注释通常用于解释数据的内容。由于数据上面直接存在文本描述非常丑陋,因此工具内嵌支持带箭头的划线工具,使得我们可以在其他恰当的地方指向数据位置,并在此处添加描述信息,解释数据内容。
我们将使用Matplotlib的注解功能绘制树形图,它可以对文字着色并提供多种形状以供选择,而且我们还可以反转箭头,将它指向文本框而不是数据点。创建名为treePlotter.py的新文件,然后输入下面的程序代码。
# 程序清单2.1.1 使用文本注解绘制树节点
import matplotlib.pyplot as plt
# 定义文本框和箭头格式
decisionNode = dict(boxstyle = "sawtooth", fc = "0.8")
leafNode = dict(boxstyle = "round4", fc = "0.8")
arrow_args = dict(arrowstyle = "<-")
# 绘制带箭头的注解
def createPlot():
fig = plt.figure(1, facecolor='white')
fig.clf()
createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
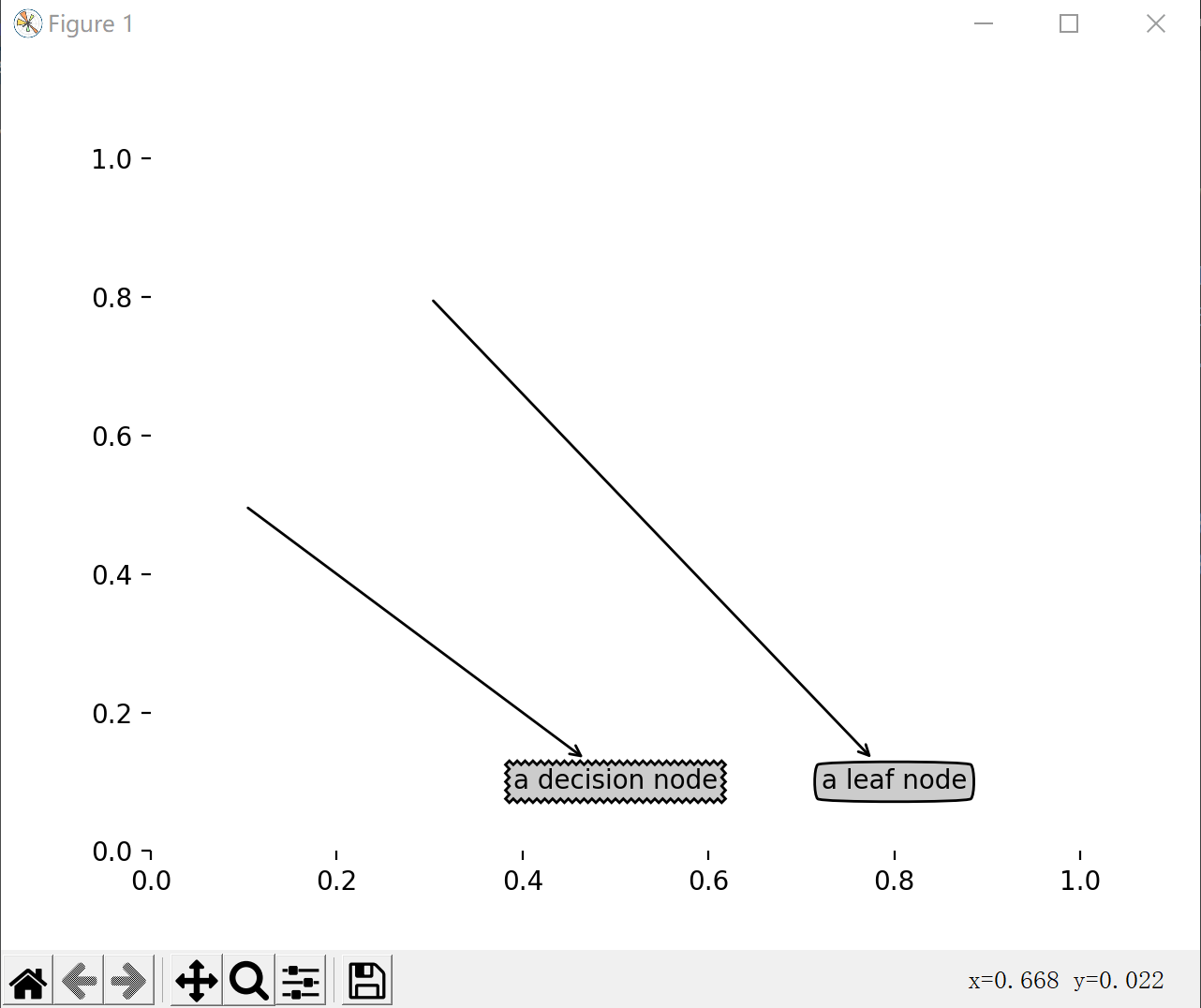
plotNode('a decision node', (0.5, 0.1), (0.1, 0.5), decisionNode)
plotNode('a leaf node', (0.8, 0.1), (0.3, 0.8), leafNode)
plt.show()
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
xytext=centerPt, textcoords='axes fraction',
va="center", ha="center", bbox=nodeType, arrowprops=arrow_args )
代码定义了树节点格式的常量①。然后定义plotNode()函数执行了实际的绘图功能,该函数需要一个绘图区,该区域由全局变量createPlot.ax1定义。最后定义createPlot()函数,它是这段代码的核心。createPlot()函数首先创建了一个新图形并清空绘图区,然后在绘图区上绘制两个代表不同类型的树节点,后面我们将用这两个节点绘制树形图。
为了测试上面代码的实际输出结果,打开Python命令提示符:
>>>treePlotter.createPlot()
2.2 构造注解树
绘制一棵完整的树需要一些技巧。我们虽然有$x$$、$$y$坐标,但是如何防止所有的树节点却是个问题。我们必须知道有多少个叶节点,以便可以正确确定$x$轴的长度;我们还需要知道树有多少层,以便可以正确确定$y$轴的高度。这里我们定义两个新函数getBumLeafs()和getTreeDepth(),来获取叶节点的数目和树的层数,参见程序清单2.2.1,并将这两个函数添加到文件treePlotter.py中。
# 程序清单2.2.1 获取叶节点的数目和树的层数
def getNumLeafs(myTree):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
# ①测试节点的数据类型是否为字典
numLeafs += getNumLeafs(secondDict[key])
else: numLeafs +=1
return numLeafs
def getTreeDepth(myTree):
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
# 测试节点的数据类型是否为字典
thisDepth = 1 + getTreeDepth(secondDict[key])
else: thisDepth = 1
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
上述程序中的两个函数具有相同的结构,后面我们也将使用到这两个函数。这里使用的数据结构说明了如何在Python字典类型中存储树信息。第一个关键字是第一次划分数据集的类别标签,附带的数值表示子节点的取值。从第一个关键字出发,我们可以遍历整棵树的所有子节点。如果子节点是字典类型,则该节点也是一个判断节点,需要递归调用getNumLeafs()函数。getNumLeafs()函数遍历整棵树,累计叶子节点的个数,并返回该数值。第2个函数getTreeDepth()计算遍历过程中遇到判断节点的个数。该函数的终止条件是叶子节点,一旦到达叶子节点,则从递归调用中返回,并将计算树深度的变量加一。为了节省大家的时间,函数retrieveTree输出预先存储的树信息,避免了每次测试代码时都要从数据中创建树的麻烦。
添加下面的代码到treePlotter.py中
def retrieveTree(i):
listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
]
return listOfTrees[i]
保存文件treePlotter.py,在Python命令提示符下输入下列命令:
>>>reload(treePlotter)
>>>treePlotter.retrieveTree(1)
{'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
>>>myTree = treePlotter.retrieveTree(0)
>>>treePlotter.getNumLeafs(myTree)
3
>>>treePlotter.getTreeDepth(myTree)
2
函数retrieveTree()主要用于测试,返回预定义的树结构。上述命令中调用getNumLeafs()函数返回值为3,等于树0的叶子节点数;调用getTreeDepths()函数也能够正确返回树的层数。现在我们可以将前面学到的方法组合在一起,绘制一棵完整的树。
更新函数createPlot()
# 程序清单2.2.2 plotTree函数
# ①在父子节点中添加文本信息
def plotMidText(cntrPt, parentPt, txtString):
xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)
# ②计算宽与高
def plotTree(myTree, parentPt, nodeTxt):
numLeafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
firstStr = list(myTree.keys())[0]
cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
# ③标记子节点属性值
plotMidText(cntrPt, parentPt, nodeTxt)
plotNode(firstStr, cntrPt, parentPt, decisionNode)
secondDict = myTree[firstStr]
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
# ④减少y偏移
for key in secondDict.keys():
if type(secondDict[key]).__name__=='dict':
plotTree(secondDict[key],cntrPt,str(key))
else:
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks
#createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses
plotTree.totalW = float(getNumLeafs(inTree))
plotTree.totalD = float(getTreeDepth(inTree))
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0
plotTree(inTree, (0.5, 1.0), '')
plt.show()
函数createPlot()是我们的主函数。绘制树形图的很多工作都是在函数plotTree()中完成的,函数plotTree()首先计算树的宽和高②。全局变量plotTree.totalW存储树的宽度,全局变量plotTree.totalD存储树的深度,我们使用这两个变量计算树节点的摆放位置,这样可以将树绘制在水平方向和垂直方向的中心位置。与程序清单2.2.1类似,函数plotTree()也是个递归函数。树的宽度用于计算放置判断节点的位置,主要的计算原则是将它放在所有叶子节点的中间,而不仅仅是它子节点的中间。同时我们使用两个全局变量plotTree.xOff和plotTree.yOff追踪已经绘制的节点位置,以及放置下一个节点的恰当位置。另一个需要说明的问题是,绘制图形的$x$轴有效范围是0到1,$y$轴有效范围也是0到1。通过计算树包含的所有叶子节点树,划分图形的宽度,从而计算得到当前节点的中心位置,也就是说,我们按照叶子节点的数目将$x$轴划分为若干部分。按照图形比例绘制树形图的最大好处是无需关心实际输出图形的大小,一旦图形大小发生了变化,函数会自动按照图形大小重新绘制。如果以像素为单位绘制图形,则缩放图形就不是一件简单的工作。
接着,绘出子节点具有的特征值,或者沿此分支向下的数据实例必须具有的特征值③。使用函数plotMidText()计算父节点和子节点的中间位置,并在此处添加简单的文本标签信息②。
然后,按比例减少全局变量plotTree.yOff,并标注此处将要绘制子节点④,这些节点即可以是叶子节点也可以是判断节点,此处需要只保存绘制图形的轨迹。因为我们是自顶向下绘制图形,因此需要一次递减$y$坐标值,而不是递增$y$坐标值。然后程序采用函数getNumLeafs()和getTreeDepth()以相同的方式递归遍历整棵树,如果节点是叶子节点则在图形上画出叶子节点,如果不是叶子节点,则递归调用plotTree()函数。在绘制了所有子节点之后,增加全局变量Y的偏移。
最后一个函数式createPlot(),它创建绘图区,计算树形图的全局尺寸,并递归调用函数plotTree()。
现在我们验证一下实际的输出效果。添加上述代码到文件treePlotter.py之后,在Python命令提示符下输入下列命令:
>>>reload(treePlotter)
>>>myTree = treePlotter.retrieveTree(0)
>>>treePlotter.createPlot(myTree)
输出效果如图,但是没有坐标轴标签。
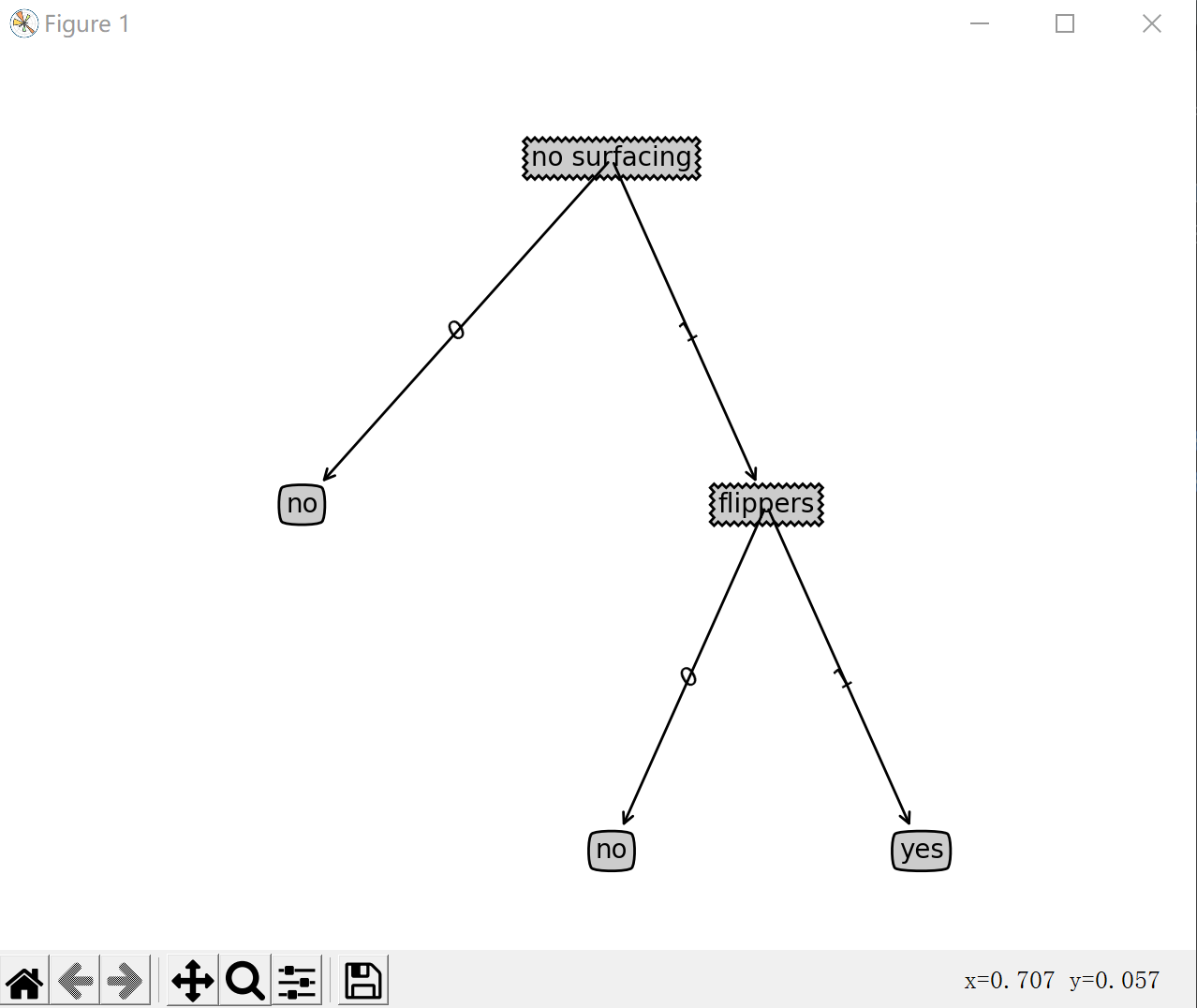
接着按照如下命令变更字典,重新绘制树形图。你也可以在树字典中随意添加一些数据,并重新绘制树形图观察输出结果的变化:
>>>myTree["no surfacing"][3]="maybe"
>>>treeplotter.createPlot(myTree)
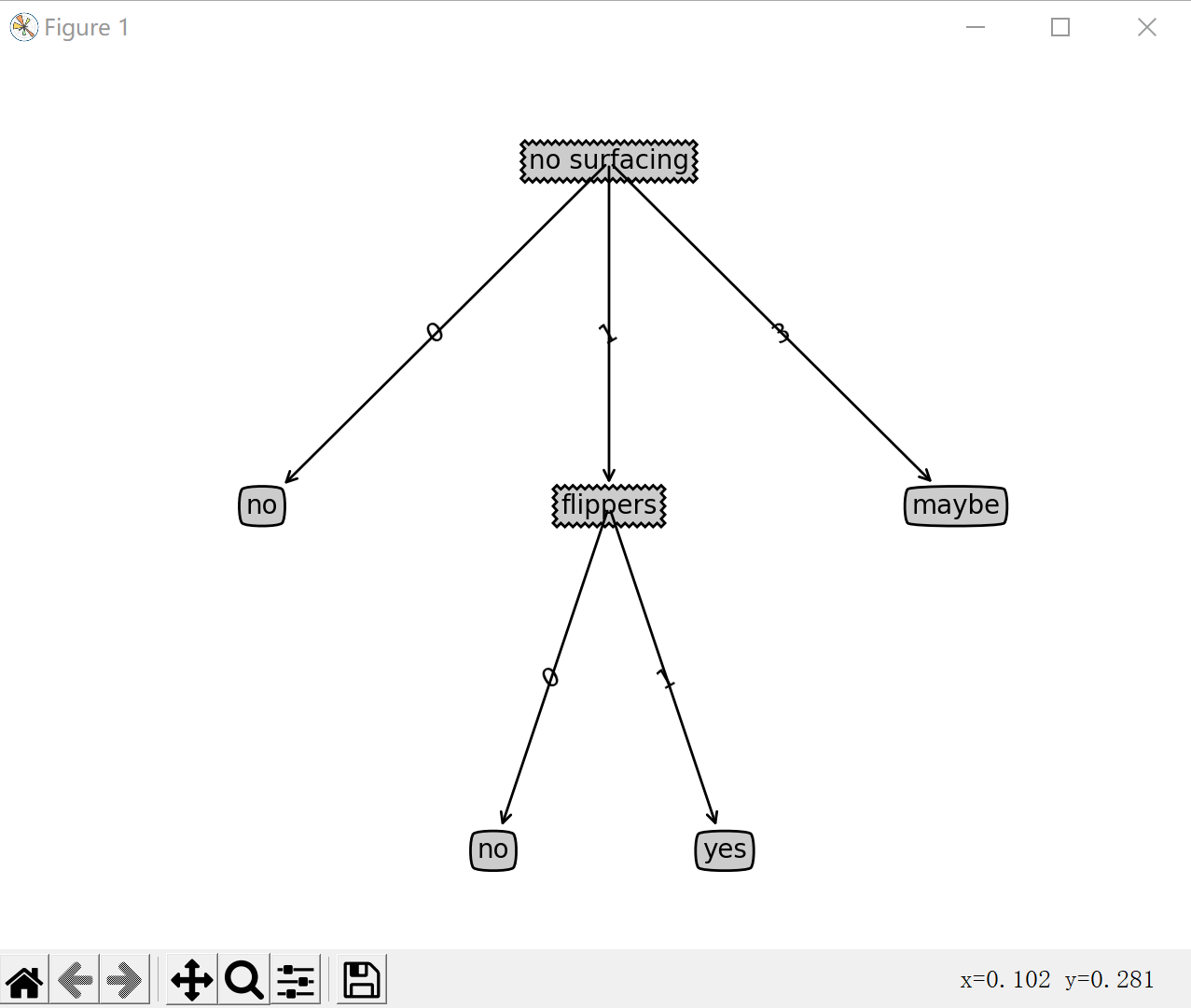
到目前为止,我们已经学习了如何构造决策树,以及绘制树形图的方法,下节我们将实际使用这些方法,并从数据和算法中得到某些新知识。